5. Phylogenetic Inference

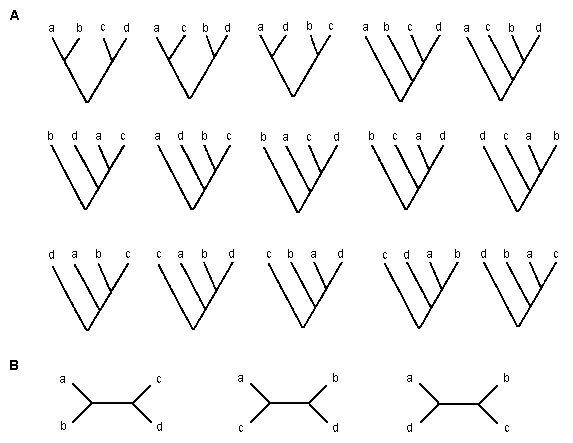
Reconstruction of the evolutionary history of genes and species is one of the most important subjects in the current study of molecular evolution. If reliable phylogenies are produced, they will shed light on the sequence of evolutionary events that generated present day diversity of genes and species and help us to understand the mechanisms of evolution as well as the history of organisms.

Species Trees and Gene Trees

Reconstruction of phylogenetic trees is a statistical problem (Cavalli-Sforza and Edwards 1967), and a tree reconstructed is an estimate of a true tree with a given topology and given branch lengths. Biologists are often interested in knowing the history of species (or population) splitting and divergence times after each splitting event. When these historical events are expressed in terms of a phylogenetic tree, this tree is called a species (or population) tree. It is usually very difficult to know the true species tree for any group of organisms, but it is possible to infer the species tree by examining the evolutionary relationships of genes from the organisms involved. A phylogenetic tree based on a gene (nucleotide or amino acid sequences) is called a gene tree. A gene tree may not agree with the species tree, because (1) nucleotide or amino acid substitution is subject to stochastic errors and (2) a gene tree is affected by sampling errors of polymorphic alleles that existed in the ancestral populations (Tajima 1983, Nei 1986, Neigel and Avise 1986, Pamilo and Nei 1988). The disagreement of gene trees and species trees may aiso occur when there are two or more copies of the same gene in the genome (Goodman et al. 1982). In general, one has to study many genes to infer a species tree.

Of course, gene trees are not studied just for inferring a species tree. In many cases, they are interesting for their own right. When one wants to know the evolutionary relationships of genes belonging to a multigene family or of polymorphic alleles within and between species, one must study gene trees.

Rooted vs. Unrooted Trees

Phylogenetic relationships of genes or organisms are usually presented in a treelike form with a root, as those in figure 5.1A. This type of tree is called a rooted tree. It is also possible to draw a tree without a root, like those in figure 5.1B. This type of tree is called an unrooted tree. The branching pattern of a tree is called a topology. There are many possible rooted and unrooted trees for a given number of species (m). In the case of m = 4, there are 15 possible rooted trees and 3 possible unrooted trees, as shown in figure 5.1. The number of possible trees rapidly increases with increasing m. In general, the number of bifurcating rooted trees for m species is given by

Fig 5.1 Fifteen possible rooted trees (A) and three possible unrooted trees (B) for four species.

There are numerous methods for constructing phylogenetic trees from molecular data (see Felsenstein 1988, Miyamoto and Cracraft 1991). They can be classified into distance methods and discrete-character methods. In distance methods, a pairwise evolutionary distance is computed for all species or OTUs to be studied, and a phylogenetic tree is constructed by certain principles and algorithms. In discrete-character methods, data with discrete character states such as nucleotide states in DNA sequences are used, and a tree is constructed by considering the evolutionary relationships of OTUs or DNA sequences at each character or nucleotide position.

It should be noted that some types of molecular data (e.g., DNA hybridization data) exist only as distance data. Therefore, phylogenetic trees for these data can be constructed only by distance methods. By contrast, discrete-character data can usually be converted into distance data. Therefore, they can be analyzed either by distance methods or by discrete-character methods. Some authors (e.g., Farris 1981, Penny 1982) have argued that distance methods are inherently inferior to discrete-character methods (e.g., parsimony methods), but their arguments are apparently based on misconceptions of distance methods (Felsenstein 1986, Nei 1987). Actually, some distance methods can be superior to discrete character methods in obtaining the correct tree, depending on the situation.

Recent computer simulations (see Nei 1991) have shown that one of the most efficient distance methods in recovering the correct topology is the neighbor-joining method proposed by Saitou and Nei (1987). Empirical studies have also shown that their method generally gives reasonable trees. Therefore, we decided to include this method in MEGA. Another distance method included in MEGA is the unweighted pair-group method with arithmetic means (UPGMA; Sneath and Sokai 1973). We included this method because of its simplicity and utility under certain circumstances. There are several other popular distance methods such as Fitch and Margoliash's (1967) method, but they are not included in MEGA because they are available in PHYLIP (Felsenstein 1993).

There are two major groups of discrete character methods, i.e., maximum parsimony methods and maximum likelihood methods. [The compatibility (Le Quesne 1969, Estabrook et al. 1975) and evolutionary parsimony (Lake 1987) methods are also discrete-character methods, but they are rarely used.] The first group of methods are included in PAUP (Swofford 1993), whereas the second are available in PHYLIP (Felsenstein 1993). Therefore, there seems to be no need to include these methods in MEGA. However, we have developed new algorithms for the maximum parsimony method for molecular data, and these algorithms seem to be quite efficient in obtaining maximum parsimony trees. We have therefore included these new algorithms in MEGA.

This method was originally proposed for taxonomic purposes, but it is possible to use it for tree building if we assume that the rate of nucleotide or amino acid substitution is the same for all evolutionary lineages. Computer simulations have shown that when the molecular clock works and the evolutionary distance is large for all pairs of OTUs, it recovers the correct tree with a reasonably high probability (Tateno et al. 1982; Sourdis and Krimbas 1987). One interesting aspect of this method is that it produces a simple tree that mimics a species tree, the branch lengths for two OTUs being the same after their separation. It is therefore appealing to biologists who are interested in constructing species trees. If this method is applied to distance data computed from many genes with large numbers of nucleotides, it is expected to give a reasonably good tree. At present, however, many investigators use relatively short sequences for phylogenetic construction, and the molecular clock often fails to work for DNA sequences. Therefore, one should be cautious about UPGMA trees. Because of the assumption of a constant rate of evolution, this method produces a rooted tree, though it is possible to remove the root for certain purposes (see section 5.6.2).

Algorithm

In this method, it is important to use a distance measure that is linearly related to evolutionary time. Once such distances are computed for all pairs of OTUs, they can be presented in the following matrix form.

OTU	1	2	3
2	d12
3	d13	d23
4	d14	d24	d34

OTU	1	2
2	d12
(34)	d1(34)	d2(34)

Here, d₁₍₃₄₎ and d₂₍₃₄₎ are given by (d₁₃ + d₁₄)/2 and (d₂₃ + d₂₄)/2, respectively. We again search for the smallest value in the new distance matrix. Suppose that d₂₍₃₄₎ is smallest. OTU 2 then joins the (34) cluster with a branch point located at distance d₂₍₃₄₎/2. In this case, OTU 1 is the last to be clustered. The branch point at which this last OTU joins the others is d₁₍₂₃₄₎/2 = [(d₁₂ + d₁₃ + d₁₄)/3 ]/2. If d₁₍₃₄₎ is smallest among the three distance values above, OTU 1 joins the (34) cluster first and then OTU 2. On the other hand, if d₁₂ is smaller than any of d₁₍₃₄₎ and d₂₍₃₄₎, OTUs 1 and 2 are clustered, and then the two clusters (12) and (34) are joined into the final single family. When more than four OTUs are involved, the above procedure is continued until all OTUs are clustered into a single family.

This method (Saitou and Nei 1987) is a simplified version of the minimum evolution (ME) method (Saitou and Imanishi 1989, Rzhetsky and Nei 1992). In the ME method, distance measures that correct for multiple hits at the same sites are used, and a topology showing the smallest value of the sum (S) of all branches (2m - 3 branches for a bifurcating tree with m OTUs) is chosen as an estimate of the correct tree. Rzhetsky and Nei (1993) have shown that when unbiased estimates of evolutionary distances are used, the true tree (topology) always gives the smallest expected value of S. Therefore, the minimum evolution method has a solid theoretical foundation. However, construction of a minimum evolution tree is time-consuming, because in principle the S values for all topologies have to be evaluated. The number of possible topologies (unrooted trees) rapidly increases with the number of OTUs. Therefore, it becomes very difficult to examine all topologies, though there are some ways to exclude all unlikely trees (Rzhetsky and Nei 1992, 1993).

In the case of the NJ method, the S value is not computed for all or many topologies, but the examination of different topologies is imbedded in the algorithm, so that only one final tree is produced. Since the algorithm of the NJ method is somewhat complicated, we shall not present it here. If the user of this program is interested in the algorithm, he or she should refer to Saitou and Nei's (1987) original paper and Studier and Keppler's (1988) slight modification. This method produces an unrooted tree, and it usually requires an outgroup OTU to find the root. In the absence of outgroup OTUs, the root is sometimes given at the midpoint of the longest route connecting two OTU's in the tree under the assumption of a constant rate of evolution. In MEGA, this practice is used unless outgroup OTUs are specified.

As mentioned above, the NJ tree is usually the same as the ME tree when the number of OTUs is small. However, if this number is large and the extent of sequence divergence is small, the topological difference between the NJ and ME trees can be substantial (Rzhetsky and Nei 1993). In this case the ME tree is obviously preferable, though the difference in S between the NJ and ME trees is usually statistically nonsignificant. In MEGA, we have not included the program for obtaining ME trees, because it requires a large amount of computer memory. A computer program (METREE) for this method is available (see Appendix E).

Maximum parsimony (MP) methods were originally developed for morphological characters, and there are many different versions (Sober 1988, Maddison and Maddison 1992, Swofford 1993). In MEGA we consider only the method that is appropriate for nucleotide sequence data, i.e., the method where evolutionary change is assumed to occur between any pair of the four nucleotides (Fitch 1971). [This is a special case of Eck and Dayhofrs (1966) method, where evolutionary change is allowed to occur between any pair of the 20 different kinds of amino acids.] In this method it is possible to give different weights to different types of substitutions (e.g., transitions and transversions, Sankoff and Cedergren 1983, Williams and Fitch 1990), but this type of modified parsimony methods will not be considered here.

The MP method is not always a consistent estimator of the true tree. [A tree-building method is said to be a consistent estimator if it gives the correct tree (topology) when an infinitely large number of nucleotides are used.] Felsenstein (1978) showed that the MP method is an inconsistent estimator when the evolutionary rate varies extensively with evolutionary lineage. Inconsistency of the MP method is known to occur even in the case of constant rate if the true tree has very short interior branches (Hendy and Penny 1989, DeBry 1992). Furthermore, even when the MP method is a consistent estimator, its efficiency of obtaining the correct tree seems to be generally lower than that of the neighbor-joining and maximum likelihood methods (Saitou and Imanishi 1989, Tateno et al. 1994). However, when (1) the extent of sequence divergence is small (d < 0.1), (2) the rate of nucleotide substitution is more or less constant, (3) there are no strong transition/transversion and G+C content biases, (4) the number of nucleotides examined is very large (more than a few thousand nucleotides), and (5) a small number of sequences are used, it seems to be a good method for estimating the true tree (Sourdis and Nei 1988, Nei 1991). Furthermore, unlike the distance or maximum likelihood method, this method is capable of using information on insertions/deletions.

For constructing an MP tree, only nucleotide sites at which there are at least two different kinds of nucleotides, each represented at least twice, are used. These sites are called parsimony-informative sites. Other variable sites are not used for constructing an MP tree, though they are informative for distance and maximum-likelihood methods.

In the MP method, the nucleotides of ancestral sequences are inferred at each nucleotide site for a given tree topology, and the minimum number of substitutions that are required to explain the nucleotide differences is counted. The sum of this number over all parsimony-informative sites of the sequences for a given topology is called the number of steps or the tree length. The tree length is then computed for all possible topologies, and the topology that shows the smallest tree length is chosen as the final tree (maximum parsimony tree). In practice, there may be two or more topologies that show the smallest tree length. These topologies are called equally parsimonious trees. The MP method is intended to find unrooted trees, and its primary goal is to determine the topology of a tree. Although it is possible to estimate branch lengths under certain assumptions (Fitch 1971, Maddison and Maddison 1992, Swofford 1993), the estimates for molecular data are usually poor unless the extent of sequence divergence is very small. Therefore, we shall not consider the estimation of branch lengths of MP trees in MEGA.

When the number of OTUs (m) is small, say m < 10, it is possible to examine all possible trees and determine the MP tree, though it can be very time-consuming. This type of search for an MP tree is called the exhaustive search. This method is not included in MEGA, because it is found in PAUP. As mentioned earlier, however, the number of topologies rapidly increases as m increases. Therefore, it is virtually impossible to examine all topologies if m is larger than 10.

There are two ways of dealing with this problem. One is to use the branch-and-bound method (Hendy and Penny 1982). In this method, the trees which obviously have a tree length longer than that of a previously examined tree are all ignored, and the MP tree is determined by evaluating the tree lengths for a group of trees that potentially have shorter tree lengths. This method guarantees finding of all MP trees, though it is not an exhaustive search. However, even this method becomes very time-consuming if m is 20 or larger. In this case one has to use another approach called the heuristic search method. In this method only a small proportion of all possible trees is examined, and there is no guarantee that the MP tree will be found. Nevertheless, it is possible to enhance the probability of obtaining the MP tree.

In the branch-and-bound method the search for an MP tree starts with a core tree of three OTUs, which has only one unrooted tree [Fig. 5.2 (A)]. Other OTUs are added to this core tree one by one according to a certain rule, and the tree length is computed at each stage of OTU addition. If the addition of an OTU to a particular branch of a core tree results in a tree length greater than a predetermined upperbound of tree length (L_U), this topology and all the subsequent topologies that can be generated by adding more OTUs to this core tree will be ignored from further consideration.

In our branch-and-bound algorithm, the initial core tree of three OTUs is chosen such that the length (L) of the tree is largest (or approximately largest) among all possible 3-0TU trees. This is to make this L closer to the length (L_M ) of the MP tree so that we can reach the MP tree faster. To obtain this initial tree, we first compute the nucleotide differences for all possible pairs of OTUs and choose the pair that shows the largest number of nucleotide differences. We then make a tree of three OTUs using this pair of OTUs and one of the remaining OTUs. For this tree, we compute the tree length using the maximum parsimony principle. This process is repeated for all the remaining OTUs, and a tree of three OTUs that shows the largest L value is chosen as the initial core tree.

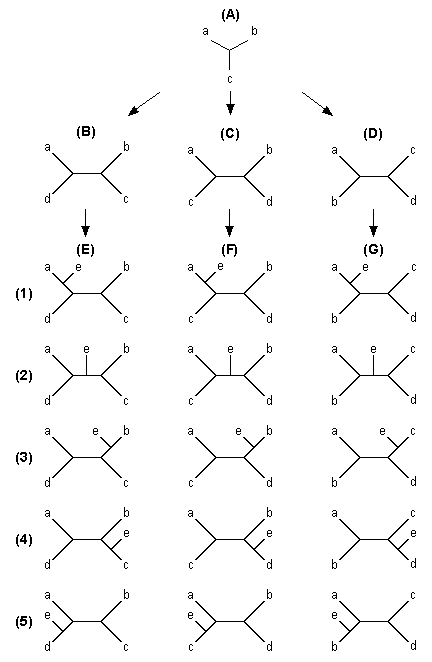Fig. 5.2 Diagrams showing the procedure of the branch-and-bound and heuristic searches

Order of OTU addition

The next step is to determine the order of OTU addition that makes the search for the MP tree faster. Our algorithm for this step is as follows. We add one of the remaining OTUs to one of the three branches of the core tree and compute the tree length by the MP procedure. We repeat the same computation for the two remaining branches and record the minimum value of the three tree lengths. We apply the same procedure for all remaining OTUs. We then find the OTU that shows the maximum value of the minimum tree lengths. This OTU is the first OTU to be added to the initial core tree. We call this procedure the maximum-of-the-minimum-values algorithm or simply the max-mini algorithm. To find the next OTU, we apply this max-mini algorithm for the remaining OTUs using the parsimony tree for the first four OTUs as the next core tree. In this case, of course, the number of minimum tree lengths to be computed for each OTU is five, because a 4-0TU tree has five branches. We can then find an OTU that shows the maximum of the minimum tree lengths. This OTU will be the second OTU to be added to the initial core tree of three OTUs. This process is repeated until the addition order of all OTUs is determined. Since the maximum of the minimum values is closer to L_M than some other value (e.g., the minimum of the minimum values), this order of OTU addition is expected to speed up the search for an MP tree.

Searching for MP tree(s)

Once the initial core tree and the order of OTU addition are determined, we are in a position to search for an MP tree. Before applying our algorithm for finding the MP tree, however, we must have a predetermined upperbound of tree length, i.e., L_U for a temporary MP tree. This value is a temporary minimum number of substitutions, which is likely to be slightly larger than the real minimum number, L_M. We determine this value by running our heuristic search program with search factor equal to 0 (see next section).

Let us now explain our algorithm with the diagrams in Fig. 5.2. We start with the initial core tree in diagram (A). In this example of five OTUs, OTUs a, b, and c form the initial core tree, and OTUs d and e are added in this order. There are three ways of adding d to the core tree [trees (B), (C), and (D)]. We first compute the tree length (L) for tree (B). If this L is greater than L_U, we ignore all the subsequent trees that are generated by adding OTU e to this tree [five trees given in column (E)]. If L < L_U or L = L_U, we add e to each of the five branches of tree (B) to form five trees with five OTUs. We again compute L for each of these five trees and find a tree (or trees), which shows the smallest L value. If this L is greater than L_U, then we move on to tree (C). However, if the L is equal to L_U, we save the tree with this L as another potential MP tree and move on to tree (C). On the other hand, if the smallest L is smaller than L_U, the tree with this L will become the next temporary MP tree, and the L_U is now replaced by this new L value. We then move to tree (C).

We apply the same procedure to tree (C) and the trees generated by adding e to tree (C). If all these trees are examined, we then move to tree (D) and its descendant trees. Since we adjust L_U whenever we find a tree with an L smaller than the previous L_U, we are assured to find the MP tree. Of course, there may be two or more equally parsimonious trees, but all these trees are identified by the present method. The same algorithm can be used for the case where the number of OTUs (m) is greater than 5. This algorithm saves computer time considerably, because many trees need not be examined if L_U is sufficiently close to the tree length (L_M ) of the true MP tree. However, even this method becomes time-consuming if m > 20.

The algorithm of our heuristic search is somewhat similar to that of the branch-and-bound method mentioned above. We start with an initial core tree of three OTUs that is determined in the same way as before. The order of OTU addition is also determined in a similar fashion except for the following. In the case of the branch-and-bound method, we computed the minimum numbers of substitutions for all OTUs for each core tree (each step of addition) and then chose the OTU that showed the maximum value among all the minimum values (max-mini algorithm). In the case of the heuristic search we choose the minimum of all the minimum values, because we are not going to do a semi-exhaustive search as in the case of the branch-and-bound method. We call this procedure the minimum-of-the-minimum-values algorithm or simply the mini-mini algorithm.

The algorithm of the search for MP trees is also similar to that of the branch-and-bound method. Let us again consider Fig. 5.2 to explain this algorithm. As before, we start with the core tree (A) and first connect OTU d to branch a to produce tree (B). We then compute the tree length (L) of this tree. We call this the local upperbound (L₁) for the first OTU addition and keep this value for future use. We then connect OTU e to branch a of tree (B) to produce tree E(1). We again compute the L value of this tree and call it the local upperbound (L2) for the second OTU addition. If there is another OTU (f) to be added, we connect this OTU to branch a of tree E(1) and obtain tree E(1, l) in Fig. 5.3. If f is the last OTU to be added, we now compute the L value not only for tree E(1, 1) but also for all other six trees that can be derived from E(1) (see Fig. 5.3). We then choose the tree that shows the smallest L value among the seven trees and call it a temporary MP tree with tree length L_U.

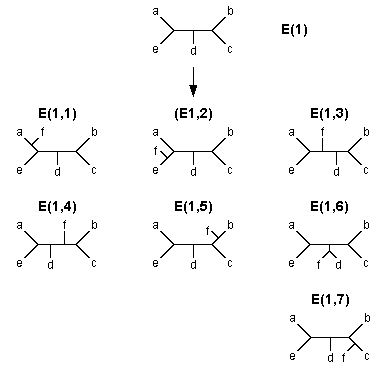Fig. 5.3 All possible trees that can be generated by adding OTU f to tree E(1)

The next step of search is to go back to tree E(2) in Fig. 5.2 and compute the L value. If this L is greater than L₂, we neglect all the trees that can be generated by adding f to this tree. If L = L₂, we compute L for all the descendant trees. If any of the trees shows an L equal to L_U, the tree is saved as another potential MP tree. If there is any tree showing an L < L_U, this tree is now considered as a new temporary MP tree, and the previous L_U is replaced by this L. By contrast, if E(2) shows an L < L₂, L₂ is replaced by this L. The L values for all descendant trees are then computed, and a new potential MP tree or a new temporary MP tree is searched for. This procedure is applied to the remaining three trees [E(3), E(4), and E(5)] of five OTUs, and the temporary MP tree (or trees) that shows the smallest L value among the 35 (= 5 x 7) trees derived from tree (B) is determined. If the above computation is completed, we now move to tree (C) in Fig. 5.2 and apply the same procedure to all trees that can be derived from this tree. Thus, if tree F(1) shows an L > L2, all seven trees derived from this tree will be ignored. However, if L = L₂, all the descendant trees are examined for their L values. If F(1) shows an L < L₂, L₂ is now replaced by this L, and we use this new L₂ for the subsequent search of an MP tree. We then compute L for all the trees derived from F(1) by adding OTU f. If there is any tree with L = L_U, it will be saved as another potential MP tree. If there is a tree with L < L_U , it becomes a new temporary MP tree, and L_U is replaced by this L. The same procedure is applied to trees F(2), F(3), F(4), and F(5) and their descendant trees. Similarly, the same procedure is applied to tree (D) and its descendant trees. If this is completed, we have the final MP tree or trees determined.

When there are more than six OTUs, essentially the same algorithm is used. The only difference is that there are many steps of OTU addition and that at each step of OTU addition the local upperbound (L₁, L₂, L₃, . . ., and L_m-4) is computed, where m is the number of sequences. L_l, L₂, L₃, ..., and L_m-4 are then used to determine whether a group of descendant trees should be ignored or not in later computations.

In this algorithm, many trees which are unlikely to have a small L value are ignored from computation of their L values, and thus the algorithm speeds up the search for the MP tree. However, the final tree or trees obtained by this algorithm may not be the true MP tree(s), because the upperbounds of the L values used here are local bounds rather than the global upperbound as used in the branch-and-bound method and the tree with the global minimum value of L may not have been obtained. There is a way to improve the efficiency of finding the MP tree. It is to increase the local upperbound at each step of OTU addition. If the local upperbound is large, the number of trees to be examined automatically increases. In the above algorithm, the local upperbound at the i-th step of OTU addition was L_i except for the first step. We now increase L_i by x_i, so that the upperbound is given by L'_i = L_i + x_i. If x_i is very large for all i's, every topology will be examined. In this case, however, the computational time will be prohibitively large. We call x_i a search factor.

We are not yet sure about the optimal values of xi's to obtain the MP tree most efficiently. Intuitively, one might argue that a rather large value of xi be given for the first few steps and a small value of x_i be given for the subsequent steps. In the above explanation of our algorithm, we examined all three topologies [tree (B), (C), and (D)] at the first step of OTU addition. This corresponds to x_l = ¥. In MEGA the user can use two different values of x_i, one for the steps before a certain specified step, which we call the transition step, and the other for all the remaining steps from and after the transition step. Our limited experience, however, has not necessarily supported the intuitive argument mentioned above. We have therefore decided to use x_i = 2 for all steps in the default option of MEGA. When search factors are large, excessive computer time may be required to complete the heuristic search. The user then should adjust the values of search factors.

Previously we mentioned that the first temporary MP tree for the branch-and-bound method is determined by the heuristic search. In MEGA, this tree is determined by using the search factors x_l = x₂ = ... = x_m-4 = 0.

It should be noted that there is no mathematical proof that the MP tree is the best estimator of the true tree. On the contrary, the MP tree is often an inconsistent estimator, as mentioned earlier. Therefore, it would be unwise to spend too much time for finding the true MP tree. When m is large, some parts of the MP tree (or any other tree) are likely to be incorrect. In this case a sub-maximum parsimony tree may serve the purpose of the investigator as well as the true MP tree does.

In the MP method, information on alignment gaps caused by insertions/deletions (indels) may be used for phylogenetic inference. In this case one gap or indel is treated as an additional character state, i.e., the fifth state for nucleotide sequences. In MEGA, this option is included. If the gaps are not given the fifth character state, they are disregarded in the computation of tree lengths. In MEGA, sites with missing information may be included in the data, but they are never used in computing tree lengths. Of course, these sites can be eliminated from the phylogenetic analysis from the beginning. Particularly when the alignment gaps are long and the sequence alignment is questionable, this option is recommended.

The MP method often produces many equally parsimonious trees. In this case, it is difficult to present all the trees for publication. One way to solve this problem is to make a composite tree that includes all the trees. Such a composite tree is called a consensus tree.

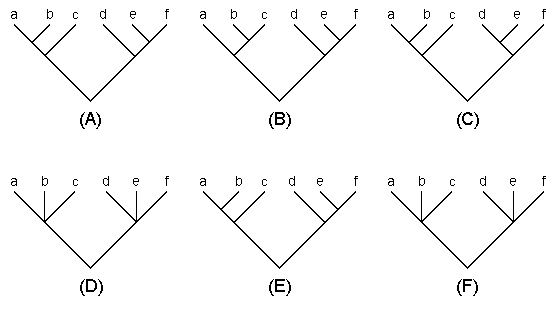
There are several different types of consensus trees (Swofford 1993), but the most commonly used are the strict consensus and majority-rule consensus trees. Let us explain these trees using the examples given in Fig. 5.4. Suppose that trees (A), (B), and (C) are three equally parsimonious trees obtained by the MP method. In a strict consensus tree any conflicting branching patterns for a set of OTUs among the rival trees are resolved by forming a multifurcating branching pattern. Thus, the strict consensus tree for trees (A), (B), and (C) are given by tree (D). Among the majority-rule consensus trees, the most commonly used is the 50% majority-rule consensus tree. In this tree a branching pattern that occurs with a frequency of >50% is adopted. In the present sample, the branching pattern ((ab)c) for OTUs a, b, and c occurs two times among the three rival trees, so this pattern is adopted. Similarly, branching pattern ((de)f) occurs two times for the other cluster. Therefore, the 50% majority-rule consensus tree is given by tree (D). It is possible to change the majority-rule percentage to any value. For example, if we use 70%, none of the branching patterns of the two 3-0TU clusters reaches 70%. Therefore, the 70% majority-rule consensus tree [tree (F)] becomes identical with the strict consensus tree. Note that the 100% majority-rule consensus tree is always identical with the strict consensus tree.

Strict consensus	50% majority-rule consensus	70% majority-rule consensus
Fig. 5.4 Examples of consensus trees

There are two different types of methods for testing the reliability of a tree obtained. One is to test the topological difference between the tree and its closely related tree by using certain quantity such as the likelihood value in the maximum likelihood method (Kishino and Hasegawa 1989) and the sum of all branch lengths in the minimum evolution method (Rzhetsky and Nei 1992). This type of test is supposed to examine the reliability of every interior branch of the tree, and it is generally a conservative test. The procedure of the test is usually quite complicated and requires a large amount of computer memory. We have therefore decided not to include it in MEGA. A computer program for the test for minimum-evolution trees is available separately (see Appendix E).

The other type of test is to examine the reliability of each interior branch whether it is significantly different from 0 or not. If a particular interior branch is not significantly different from 0, we cannot exclude the possibility of trifurcation of the branches associated or even the other types of bifurcating trees that can be generated by changing the splitting order of the three branches involved. There are two different ways of testing the reliability of an interior branch. One way is to compute the standard error of the interior branch and test the deviation of the branch length from 0, and the other is to use the bootstrap test (Efron 1982, Felsenstein 1985). These tests are included in MEGA.

Since the statistical properties of NJ trees are better understood than those of UPGMA and MP trees, let us first discuss the test of these trees. In MEGA, the standard error test of NJ trees is conducted following Rzhetsky and Nei's (1992, 1993) method. That is, once an NJ tree is obtained by the Saitou-Nei algorithm, the branch lengths of the tree are re-estimated by using the ordinary least squares method, and the standard errors of the estimates are computed. Let b and s(b) be an estimate of an interior branch length and its standard error, respectively. The statistical significance of b from 0 is then tested by the t-test [t = b/s(b)] with degrees of freedom ¥. In the standard statistical test, a null hypothesis is tested by computing the probability of Type I error (a; significance level). In MEGA, however, the complement of this probability (1 - a) is computed. We call this the confidence probability (CP). Therefore, the reliability of a branch length is high when CP is high. Usually, if CP > 0.95 or 0.99, the branch length is considered to be statistically significant.

In bootstrap tests, the same number of nucleotides as the actual number used for constructing the NJ tree are randomly sampled with replacement from the original sequence data, and an NJ tree is produced from this set of resampled nucleotide data. The topology of the tree is then compared with the original NJ tree. Any interior branch of the NJ tree that gives the same partition of sequences as that of the bootstrap tree (see Penny and Hendy 1985, Rzhetsky and Nei 1992 for partition of sequences) is given value 1 (identity value), whereas other interior branches are given 0. This process is repeated several hundred times, and the percentage of times each interior branch of the NJ tree receives identity value I is computed. We call this the bootstrap confidence level (BCL). Note that this test is different from that included in PHYLIP, where a bootstrap consensus tree is constructed.

The statistical properties of the bootstrap test are complicated and are not well understood (Zharkikh and Li 1992a, b, Felsenstein and Kishino 1993, Hillis and Bull 1993). When the test is applied to an NJ tree, however, the interpretation of the test results is simpler. If (1) every site of the DNA sequence evolves in the same way, (2) the distance measure used is an unbiased estimator of the number of nucleotide substitutions, and (3) the numbers of sequences and nucleotides used are sufficiently large, the null hypothesis of the bootstrap test is that the length of each interior branch is 0, and the BCL of a branch approximately measures the probability of the branch length being different from 0 at least when the BCL > 0.9. Computer simulations have shown that the BCL is indeed very close to the equivalent probability (CP) determined by the standard error test mentioned above when BCL > 0.9 (T. Sitnikova, unpublished results). Of course, for this interpretation to be correct, the original sequence data should contain a substantial number of nucleotides. If this number is small and happens to be a biased sample from a long sequence that is under investigation, bootstrap resampling will never be able to correct the bias (Nei 1991, Zharkikh and Li 1992a).

The bootstrap test for NJ trees is known to be conservative if an unbiased distance measure is used (M. Nei and S. Kumar in Nei and Rzhetsky 1991). However, if biased distance measures are used, this test may lead to an incorrect conclusion and an incorrect topology may receive a high BCL value. Therefore, it is important to use proper distance measures for this test.

Nei et al. (1985) developed a method for computing the standard errors of interior branch lengths for a UPGMA tree under the assumption of constant rate of evolution. However, their method is not easy to apply when the number of sequences is large. Furthermore, if the rate of nucleotide substitution is not constant, their test may give an erroneous conclusion. Therefore, we have not included it in MEGA.

Instead, we have included the bootstrap test. In this test, the root of UPGMA trees is eliminated, and both the original and bootstrap trees are treated as unrooted trees. The procedure of the test is the same as that for NJ trees, and each interior branch of the original UPGMA tree receives the BCL value.

If the rate of nucleotide substitution is constant for all evolutionary lineages and the assumptions mentioned for UPGMA are all satisfied, the BCL is again expected to give the probability of each interior branch length being different from 0 when BCL is high. This is because UPGMA gives unbiased estimates of branch lengths under this condition if the topology obtained is correct (Chakraborty 1977).

In practice, however, the rate of nucleotide substitution is not necessarily constant, and there is increasing evidence that the rate often varies from lineage to lineage. Furthermore, the probability of obtaining the correct topology by UPGMA is generally lower than that by the NJ method even if the rate of nucleotide substitution is constant (Saitou and Nei 1987). In these cases, the bootstrap test may lead to an incorrect conclusion. Particularly when the rate of nucleotide substitution varies with evolutionary lineage, an incorrect branching pattern may receive a high bootstrap value. Therefore, one should be cautious about the bootstrap test of UPGMA trees.

It is very difficult to develop a solid statistical test for MP trees, because the stochastic nature of nucleotide substitution is not taken into account in obtaining these trees. Although it is possible to estimate branch lengths, the estimates are usually biased downward. Therefore, the standard error test cannot be applied.

As mentioned earlier, the MP method may give a reasonably good tree under certain conditions. In this case, it is meaningful to conduct a bootstrap test. Felsenstein (1985) proposed a bootstrap test for an MP tree, but his test is different from ours. While we are interested in testing the accuracy of an MP tree obtained, his test is for examining the accuracy of a bootstrap consensus tree. We have initiated implementation of our test for an MP tree in MEGA but decided not to include it in the present version, because it is still in a preliminary stage. We plan to include it in the next version. Here, we briefly describe the strategy and algorithm of our bootstrap test.

We first note that if the MP method produces a large number of equally parsimonious trees for a given set of sequence data (e.g., Hedges et al. 1992), there is no need to conduct a statistical test, because in this case we cannot choose the best tree or a few best trees anyway. Second, if the number of OTUs is so large that we have to use the heuristic search, the bootstrap test is not very meaningful, because we are not sure whether the tree obtained is the MP tree. In MEGA, therefore, we will consider only the case where the number of OTUs is relatively small (say m < 20) and the number of equally parsimonious trees is one or a few.

In our approach, we first determine all MP trees for a given set of data using the branch-and-bound method. If there is only one global MP tree, we keep this tree and examine the reliability of the tree by using the bootstrap test. In this case, it is possible that in a particular bootstrap replication two or more equally parsimonious trees will appear. We then compare each of these trees with the global MP tree obtained from the entire data set and determine the identity value 1 or 0 for a given interior branch of the global MP tree compared with each of the bootstrap MP trees. For each interior branch of the global MP tree, the sum of identify values over all bootstrap MP trees is then divided by the number of the latter trees for this particular bootstrap replication. Thus, if all the bootstrap MP trees for a particular bootstrap replication show the same partition of sequences as that of the MP tree for a given interior branch, this branch receives value 1 for this replication. This procedure is repeated for all bootstrap replications. We can then compute the BCL values for all interior branches of the global MP tree. When there are several global MP trees obtained from the entire data set, we construct a strict consensus tree for them and regard it as a single global MP tree. We can then apply the same procedure as that mentioned above and compute the BCL values for all interior branches of the global MP tree.

In the case of the MP method, the BCL value of an interior branch is unlikely to be equal to the probability that the length of the branch is different from 0 even when the sequence data favorable for the MP method are used (see section 5.5). However, a BCL value higher than 95 percent probably gives some confidence of the branching pattern associated with the branch [see Zharkikh and Li (1992a) for the special case of four sequences].

However, when the sequence data do not satisfy the condition required for the MP method and this method gives an inconsistent tree, a bootstrap test may give a false confidence for the tree obtained (Zharkikh and Li 1992b). That is, even an incorrect branching pattern may receive a BCL value of 100 percent if the number of nucleotides examined is large. Therefore, the user of this test should always be cautious about the interpretation of the BCL values. We suggest that when a tree topology is estimated by the MP method, the branch lengths of the topology should also be estimated by some other method such as the NJ, ME, and maximum likelihood methods. Information on branch lengths will give some idea about the accuracy of the bootstrap test for an MP tree. Note also that if the number of informative sites used is small, bootstrap tests may give erroneous conclusions.

When a phylogenetic tree has low CP or BCL vaiues for several interior branches, it is often useful to produce a multifurcating tree by assuming that all such interior branches have a branch length equal to 0. We call this multifurcating tree a condensed tree. In MEGA, this condensed tree can be produced for any level of CP or BCL value. For example, if there are several branches with CP or BCL values of less than 50% , a condensed tree with the 50% CP or BCL level will have a multifurcating tree with all these branch lengths reduced to 0.

Since the branches of low significance are eliminated to form a condensed tree, this tree gives emphasis on reliable portions of branching patterns. However, this tree has one drawback. That is, since some branches are reduced to 0, it is difficult to draw a tree with proper branch lengths for the remaining portion. We have therefore decided to give our attention only to the topology. Thus, the branch lengths of a condensed tree in MEGA are not proportional to the number of nucleotide or amino acid substitutions.

Note that condensed trees are different from consensus trees mentioned earlier, though they may look similar in practice. A consensus tree is produced from many equally parsimonious trees, whereas a condensed tree is merely a simplified version of a tree. A condensed tree can be produced for any type of tree (NJ, ME, UPGMA, MP, or maximum-likelihood tree).

It should be noted that any statistical test of topological differences or branch lengths depends on a number of assumptions, which are not always satisfied by actual data, and that when the assumptions are not satisfied an incorrect tree may be statistically supported even when the NJ, ME, or the maximum-likelihood method are used (Tateno et al. 1994). Therefore, when the pattern of nucleotide or amino acid substitutions for the data set used is complicated, one should be cautious about the interpretation of the results of statistical tests. As a general rule, it is safe not to trust results based on a relatively small number of nucleotides even if every interior branch of an estimated tree is significant at the 95% CP or BCL. These results should be confirmed by increasing the number of nucleotides if possible.

Particularly for establishing evolutionary relationships of different organisms, it is important to examine a large number of nucleotides from many different genes, because different genes may be subject to different evolutionary forces. Furthermore, if a large number of nucleotides are used, there is no need to use a sophisticated and time-consuming tree-building method. A simple method like the NJ method usually gives the same tree as that obtained by time-consuming statistical methods.